Calibration Basics Part IV - Measurement Uncertainty

This is Part IV of our Calibration Basics Series. 

In Part I, we looked into the general overview of what calibration is. While a rather simple concept, it is still extremely important to keep those basics straight.

In Part II, we dove into what happens when your calibration process finds a piece of equipment to be reading off.

In Part III, we discussed the most important cornerstone affecting accuracy in calibration, traceability.

---

If you have been reading along, you now have a firm understanding on exactly what calibration is, where adjustment fits into the calibration process and how traceability is the most important cornerstone in the calibration process.

However, as mentioned in the traceability segment, all of those steps in the process provide us accuracy within an acceptable uncertainty range. So what is this uncertainty range anyways?

Measurement Uncertainty

Let's return to our bathroom scale example. As mentioned the standards (weights) used to compare to the scale's readings fundamentally need to be considerably more precise than the scale itself.

To understand this better, consider this. There never has, nor will there ever be an exactly perfect measurement (except for random chance). This is because each measurement taken only reads out to a certain number of decimal places.

In other words, even if we were to measure a 1" piece of steel (a gage block) at 1.000”, there is a decent chance that if we took this reading out even just one more decimal point, it may read 1.0001”, thus not exactly one inch.

Sources of Measurement Uncertainty

Let's take a brief look into what causes this uncertainty. There are two main categories of measurement errors:

• Systematic
• Random

Systematic Error

Systematic sources of error are simply that, systematic. They occur predictably and are typically constant or proportional to the true value. This error is often correlated with accuracy. Some common examples of systematic error in this context are:

• Accuracy of the measuring device
• Environmental conditions

The good news is that if the cause of the systematic error can be identified, then it usually can be eliminated or accounted for.

Random Error

Similarly, random error is also, just that, random. They always present in a measurement and can vary drastically from the same, repeated measurement. This error is often correlated with precision. Some common examples of random error in this context are:

• Operator skill
• Slop in the measurement apparatus

Unfortunately cannot be accounted for as easily. It can, however, be estimated comparing multiple measurements and reduced by averaging the variance in these measurements.

More information on measurement uncertainty can be found in the Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME).

Measurement Uncertainty in Calibration

Now that we understand how and why there will always be some error (uncertainty) in every measurement, let's take a look at how this affects calibration. To do so, we will revisit our bathroom scale example.

Even the most pricey bathroom scales on the market today only have an accuracy of 0.1 pounds. This is simply because nobody really needs to know how much they weight to any higher degree of precision.

Now, what would happen if we were to attempt to calibrate this scale with something that had an accuracy of +/- 0.5 pounds? We would NEVER know if the scale was actually within its accuracy range.

Here is an example. Say you were testing the scale at 100 pounds. Let's assume we are using a 100 pound weight with a 0.5 pound accuracy. This means it means the actual weight could be anywhere from 99.5 to 100.5. If we were to use this on a scale with a 0.1 pound accuracy and get a reading of 100 pounds on the scale, in order to pass calibration the reading must fall between 99.9 and 100.1 pounds. We could only statistically prove the scale is reading between 99.5 and 100.5 pounds, thus not allowing the scale to pass calibration, even if it were reading perfectly.

This is because of measurement uncertainty. Since the accuracy of the equipment used is part of the systematic error in a measurement uncertainty, the uncertainty of this calibration is already larger than the accuracy of the scale.

Test Uncertainty Ratio

The good news is, there is an answer for this, the test uncertainty ratio (or TUR for short). What this states is that each piece of equipment that is used to measure another, must be significantly more accurate than the instrument it is measuring.

Traditionally, the test uncertainty ratio has been defined as a 10:1 ratio. What this means is that the standard used to calibrate a piece of measuring & test equipment (M&TE) must be 10 times more accurate.

An example of what this might look like is:

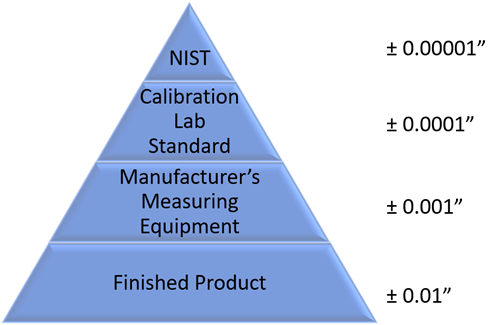
Here is how this works:

1. A finished product is produced by a manufacturer. It has a design feature that needs to be within +/-0.01" of a specific size.
2. The manufacturer checks that attribute with a gage that has an accuracy of +/- 0.001".
3. A calibration lab calibrates that gage with a standard that is accurate to +/- 0.0001".
4. The calibration lab's standard is compared to the NIST standard that is accurate to +/- 0.00001".

As you can likely see, this all but eliminates the accuracy of a piece of equipment from the measurement uncertainty equation, as the net effect it has on the outcome of the measurement is negligible.

In fact, it is so small, that it is now more common to see the TUR defined as 4:1. This prevents from gaging "overkill" - purchasing more precise (expensive) gaging than what is actually required.

Now, keep in mind, there are still many other sources of measurement uncertainty (such as temperature, gage repeatability, etc.). But don't worry. The good news is, you don't have to worry about this. By using an ISO 17025 accredited calibration provider, such as Fox Valley Metrology, measurement uncertainty is already factored into your calibration findings.

As can be seen on our certificates, we automatically provide you with measurement uncertainty for every single reading we take. Additionally, it is already factored into the calibration findings so we don't run into the bathroom scale issues presented above.

---

You may be asking, "But wait, you mentioned the accuracies (tolerances) of measuring and test equipment. What the heck are those?" Learn all about this concept and more in Part V of our Calibration Basics Series.